近日，北京大学先进制造与机器人学院李忠奎教授课题组在移动机器人运动规划领域取得新进展，针对移动机器人中广泛存在的非完整约束与曲率约束，通过协同设计两组方程——曲率约束向量场与饱和跟踪控制律，实现了非完整系统在曲率约束下到目标位形（目标位置+目标姿态）的近全局收敛。该研究成果以“Curvature-Constrained Vector Field for Motion Planning of Nonholonomic Robots”为题，近期发表在国际机器人领域顶刊《IEEE Transactions on Robotics (T-RO)》（DOI：10.1109/TRO.2025.3644358）。

在自动驾驶与移动机器人领域，泊车问题本质上是一个典型的非完整约束与曲率约束下的运动规划问题 。尽管人类司机能够凭借直觉轻松泊车，但要用数学语言在保证100%成功率的前提下刻画这一过程却非易事 。非完整约束作为一种“以自由度换性能”的权衡，广泛存在于各类轮式车辆与固定翼飞机：通过限制系统的侧向位移，换取了在高速巡航和重载运输上的优势 。然而，这种机制也内在地限制了转向能力，使得机器人必须在有界的曲率范围内规划路径 。这就好比汽车无法像螃蟹一样横着走，也无法在狭窄胡同里原地掉头 。这种“不能横移”与“转弯半径受限”的双重约束，极大地压缩了运动规划的可行解空间，导致传统的运动规划算法在极端初始条件下往往难以收敛，或生成的轨迹无法被实际执行。

非完整约束不允许车辆横向移动

曲率约束阻碍窄路掉头

针对上述挑战，李忠奎教授课题组提出了一种全新的解决思路：不再单纯依赖复杂的路径搜索，而是去跟踪一个内嵌物理约束的向量场 。该研究的核心包括两部分：一是曲率约束向量场（Curvature-Constrained Vector Field, CVF），研究团队针对一系列基本流场，给出了一种曲率约束下的混合策略，混合所得的向量场能够为非完整机器人指定期望朝向，提供满足曲率限制的参考轨迹 ；二是饱和控制与动态增益，为了确保机器人在跟踪向量场时不违背曲率约束，团队为角速度控制律设定了饱和上界，并基于向量场在机器人运动下的变化趋势，同时对角速度增益进行动态调整 。上述方法通过“协同设计”——控制律的饱和情况确定向量场设计参数，而向量场变化趋势动态调节控制律增益，巧妙地解决了“规划”与“控制”的脱节问题 。研究团队从理论上证明了：非完整系统能在满足曲率约束的前提下，从几乎任意初始位形（位置+姿态）收敛至目标位形。

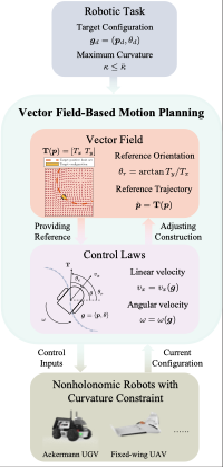
算法框架图

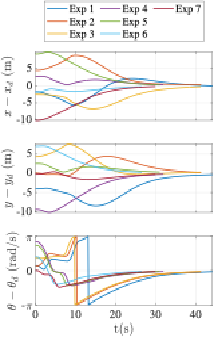
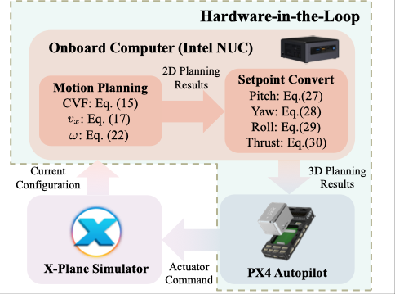
为了验证方法的有效性，研究团队进行了大规模的蒙特卡洛仿真与实物实验。仿真表现显示，在随机给定的初始/目标位形测试中，所提算法实现了100%的收敛成功率，显著优于现有算法 。在阿克曼无人车实验中，在非完整与曲率约束下，对于多组给定的初始与目标位形，无人车均能渐进收敛至目标 。此外，该算法同样适用于三维空间中的固定翼无人机，展示了较好的通用性 。实验结果表明，该算法理论严谨，针对实际工况下的不确定性与外界扰动具备良好的鲁棒性，且计算负荷低，能基于板载计算资源进行实时运算，具有较好的工程应用价值。

对比结果（CVF为所提方法）

阿克曼车实验结果（左上：实验1-3轨迹，左下：实验4-7轨迹，右：实验1-7收敛结果）

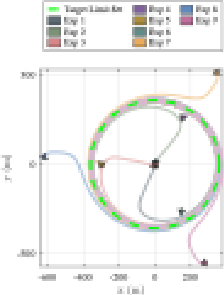无人机实验结果（左：半实物实验环境，右：实验结果）

该论文的第一作者为北京大学先进制造与机器人学院博士生乔亦可，合作者包括北京科技大学副教授贺晓东、北京大学博士生卓安、北京大学研究员孙志勇、中国科学院院士包为民。北京大学先进制造与机器人学院李忠奎教授为通讯作者。该成果得到了国家自然科技基金和北京市自然科技基金项目的支持。

论文链接：https://ieeexplore.ieee.org/document/11300826